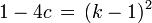|
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.
|
| Description |
English: Diagram showing the connexion between Verhulst dynamic and Mandelbrot set
|
| Date |
7 April 2008 |
| Source |
Own work |
| Author |
Georg-Johann Lay |
Permission
( Reusing this file) |
| Public domainPublic domainfalsefalse |
 |
I, the copyright holder of this work, release this work into the public domain. This applies worldwide.
In some countries this may not be legally possible; if so:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.Public domainPublic domainfalsefalse
|
|
Note
The Verhulst process
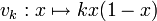
is equivalent to the process
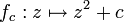
by means of a linear transformation 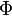 , i.e.
, i.e.
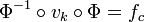
Just let
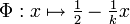
and observe that the Parameters  and
and 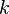 are connected via
are connected via
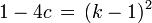
File usage
The following pages on Schools Wikipedia link to this image (list may be incomplete):
SOS Childrens Villages has brought Wikipedia to the classroom. SOS Children's Villages cares for children who have lost their parents. Our Children's Villages give these children a new home and a new family, while a high-quality education and the best of medical care ensures they will grow up with all they need to succeed in adult life. Sponsoring a child is the coolest way to help.



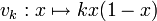
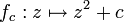
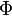 , i.e.
, i.e.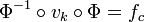
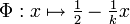
 and
and 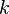 are connected via
are connected via